Business Mathematics, Solved Paper, 2010, FBISE ICOM I, MCQS, Short Questions, Extensive Questions

Business Mathematics, Solved Paper, 2010, FBISE ICOM I, MCQS, Short Questions, Extensive Questions
Leave a Comment / Business Mathematics / By

In this post, we are going to discuss, Business Mathematics, Solved Paper, 2010, FBISE ICOM I, MCQS, Short Questions, Extensive Questions. If you want to read the solved papers of Business Statistics ICOM II of FBISE, BISELHR, BISERWP and other boards, just explore the resource of the site. All the papers and reading resource including solved papers from intermediate, O, A level, graduation and masters level is given the website.

Table of Contents

Business Mathematics, Solved Paper, 2010, FBISE ICOM I, MCQS, Short Questions, Extensive Questions

Solved & Written by Iftikhar Ali M.Sc Economics, M.Com (Finance) Lecturer Statistics, Accounting and Finance

MCQS

Q.1 Circle the Correct Option i.e. A/B/C/D. Each Part Carries 1 Mark.
(i)Gain from a T.V Set of Rs. 4000/- sold at the profit of 20 percent is:
 A. Rs. 750B. Rs. 800C. Rs. 600D. Rs. 900 
      
(ii)A ratio can be reduced to its:
 A. Highest termB. Lowest termC. Middle termD. None of these 
      
(iii)Every percentage can be converted into:
 A. Decimal fractionB. RatioC. ProportionD. Both A & B 
      
(iv)Commission on the deal of Rs. 6000 @ 3%. What is the amount of deal?
 A. Rs. 60,000B. Rs.100,000C. Rs. 150,000D. Rs. 200,000 
      
(v)At what simple interest rate an amount triples itself in 6 years?
 A. 10%B. 20% C. \[ \mathbf{33}\frac{\mathbf{1}}{\mathbf{3}}\mathbf{\%}\ \]D. None of these 
  
(vi)If h(x) = \ \frac{1}{x - 5}\  then h(5) will be:
 A. DefinedB. FiniteC. InfiniteD. None of these 
      
(vii) ax + by + c = 0\  is the linear equation in variable:
 A. Consistent\ B. \mathbf{Inconsistent}\ C. Identical\ D. Homogenous\  
      
(viii)Number of rows and number of column:
 A. Must be equalB. May equalC. May not equalD. May or may not equal 
      
(ix)The inverse of matrix \begin{pmatrix}3 & 6 \\7 & 14 \\\end{pmatrix}\
 A. \begin{pmatrix}14 & -6 \\7 & 3 \\\end{pmatrix}\ B. \begin{pmatrix}3 & 6 \\7 & 14 \\\end{pmatrix}\ C. \begin{pmatrix}\mathbf{0}& \mathbf{0} \\\mathbf{0} & \mathbf{0} \\\end{pmatrix}\ D. None of these 
      
(x)While converting binary fraction 101.1, the .1 is converted into:
 A. 2^{0}\ B. \mathbf{2}^{\mathbf{- 1}}\ C. 2^{- 2}\ D. 2^{- 3}\  

Short Questions

Section B

Q.2 Attempt any eight parts. All parts carry equal marks. (3 x 8) = 24

(i) If the stay of 12 men for 28 days in a hotel cost Rs. 6720/-. Find the cost of stay of 8 men for 14 days.

Solution

\begin{matrix}\mathbf{Men} & \mathbf{Days} & \mathbf{Cost} \\\mathbf{12} & \mathbf{28} & \mathbf{6720} \\\mathbf{8} & \mathbf{14} & \mathbf{x} \\\end{matrix}\

\mathbf{\ \ \ }\frac{\mathbf{12}}{\mathbf{8}} \frac{\mathbf{28}}{\mathbf{14}} \frac{\mathbf{6720}}{\mathbf{x}}\

\mathbf{x(28 \times 12)\ = \ 6720\ \times \ 14\ \times \ 8}\

\mathbf{336}\mathbf{x\ = \ 752640}\

\mathbf{x =}\frac{\mathbf{752640}}{\mathbf{336}}\mathbf{= 2240}\

(ii) If the 16% increase in the basic salary of a government employee will become Rs. 3248/- per month. What is his salary before the increase?

Solution

Salary after 16% increase = 3248

\mathbf{Salary\ before\ increase = \ }\frac{\mathbf{3248}}{\mathbf{116}}\mathbf{\ \times \ 100 = 2800}\

(iii) a. Three partners invested Rs. 18000, Rs. 16500 and Rs. 12500, respectively. When profit was distributed the third one got Rs. 4625/-. Find the total profit earned.

b. At what rate Rs. 5000/- will be doubled in 5 years?

Solution

(a)

InvestmentsA’s InvestmentB’s InvestmentC’s Investment
180001650012500
Simplified Ratio363325

Ratios of Partners = 36:33:25

Sum of ratios = 36 + 33 + 25 = 94

Third Partner C got profit of Rs. 4625 which is 25 equal proportions

\mathbf{One\ portion\ of\ the\ profit\ = \ }\frac{\mathbf{4625}}{\mathbf{25}}\mathbf{= 185}\

\mathbf{Total\ Profit\ = \ 185\ \times \ 94\ = \ 17390}\

(b)

\mathbf{P\ = \ 5000,\ A\ = \ 10,000,\ T\ = \ 5,\ R\ = \ ?}\

\mathbf{As\ we\ know\ that\ S.I\ = \ A\ -\ P\ = \ 10,000\ -\ 5000\ = \ 5000\ So}\

\mathbf{S.I\ = \ PRT}\

\mathbf{5000\ = \ 5000\ \times \ R\ \times \ 5}\

\mathbf{5000\ = \ 25000\ R}\

\mathbf{R\ =}\frac{\mathbf{5000}}{\mathbf{25000}}\mathbf{\ = \ 0.2}\

\mathbf{R\ = \ 0.2\ \times \ 100\ = \ 20\%}\

(iv) Draw the graph of the following quadratic function

Solution

Given Function

\mathbf{f(x)\ = \ 5\ + \ 2}\mathbf{x\ - \ x²}\

\mathbf{Here\ a\ = \ - 1,\ b\ = \ 2\ \&\ c\ = \ 5}\

Since a < 0, parabola opens downward.

Let y is a function of x:

\mathbf{y = f}\left( \mathbf{x} \right)\mathbf{=}\mathbf{5\ + \ 2}\mathbf{x\ - \ x²}\

\mathbf{y = f}\left( \mathbf{- 3} \right)\mathbf{=}\mathbf{5\ + \ 2}\left( \mathbf{- 3} \right)\mathbf{-}\left( \mathbf{- 3} \right)^{\mathbf{2}}\mathbf{= 5 - 6 - 9 = - 10}\

\mathbf{y = f}\left( \mathbf{- 2} \right)\mathbf{=}\mathbf{5\ + \ 2}\left( \mathbf{- 2} \right)\mathbf{-}\left( \mathbf{- 2} \right)^{\mathbf{2}}\mathbf{= 5 - 4 - 4 = - 3}\

\mathbf{y = f}\left( \mathbf{- 1} \right)\mathbf{=}\mathbf{5\ + \ 2}\left( \mathbf{- 1} \right)\mathbf{-}\left( \mathbf{- 1} \right)^{\mathbf{2}}\mathbf{= 5 - 2 - 1 = 2}\

\mathbf{y = f}\left( \mathbf{0} \right)\mathbf{=}\mathbf{5\ + \ 2}\left( \mathbf{0} \right)\mathbf{-}\left( \mathbf{0} \right)^{\mathbf{2}}\mathbf{= 5 + 0 - 0 = 5}\

\mathbf{y = f}\left( \mathbf{1} \right)\mathbf{=}\mathbf{5\ + \ 2}\left( \mathbf{1} \right)\mathbf{-}\left( \mathbf{1} \right)^{\mathbf{2}}\mathbf{= 5 + 2 - 1 = 6}\

\mathbf{y = f}\left( \mathbf{2} \right)\mathbf{=}\mathbf{5\ + \ 2}\left( \mathbf{2} \right)\mathbf{-}\left( \mathbf{2} \right)^{\mathbf{2}}\mathbf{= 5 + 4 - 4 = 5}\

\mathbf{y = f}\left( \mathbf{3} \right)\mathbf{=}\mathbf{5\ + \ 2}\left( \mathbf{3} \right)\mathbf{-}\left( \mathbf{3} \right)^{\mathbf{2}}\mathbf{= 5 + 6 - 9 = 2}\

\mathbf{y = f}\left( \mathbf{4} \right)\mathbf{=}\mathbf{5\ + \ 2}\left( \mathbf{4} \right)\mathbf{-}\left( \mathbf{4} \right)^{\mathbf{2}}\mathbf{= 5 + 8 - 16 = - 3}\

\mathbf{y = f}\left( \mathbf{5} \right)\mathbf{=}\mathbf{5\ + \ 2}\left( \mathbf{5} \right)\mathbf{-}\left( \mathbf{5} \right)^{\mathbf{2}}\mathbf{= 5 + 10 - 25 = - 10}\

X-3-2-1012345
Y-10-325652-3-10
Business Mathematics, Solved Paper, 2010, FBISE ICOM I, MCQS, Short Questions, Extensive Questions

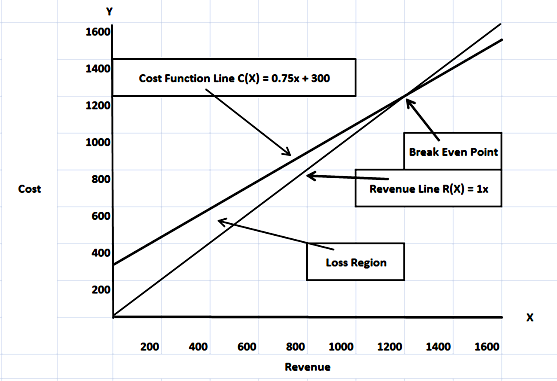
(v) A manufacturer produces items at spending 75 paisa per item daily & sells them for Rs. 1 per item. His daily operational cost is Rs. 300/- What is break-even point? Graph your results.

Solution

Units Produced = x, Revenue function = R(x), Cost Function = C(x) so

\mathbf{R(x)\ = \ 1}\mathbf{x\ \&\ C(x)\ = \ 0.75}\mathbf{x\ + \ 300}\

As we know that at break-even point firm gets zero profit & Profit P(x) =R(x) – C(x) so assuming zero profit equation of break-even will be:

\mathbf{P(x)\ = \ R(x)\ -\ C(x)}\

\mathbf{0\ = \ 1}\mathbf{x\ -\ (0.75}\mathbf{x\ + \ 300)}\

\mathbf{1}\mathbf{x\ -\ 0.75}\mathbf{x\ -\ 300\ = \ 0}\

\mathbf{0.25\ x\ \ = \ 300}\

\mathbf{X\ =}\frac{\mathbf{300}}{\mathbf{0.25}}\mathbf{\ = \ 1200\ units}\

Now put X units 1200 in revenue & cost function

\mathbf{R(x)\ = \ 1}\mathbf{x\ = \ 1(1200)\ = \ 1200}\

\mathbf{C(x)\ = \ 0.75}\mathbf{x\ + \ 300\ = \ 0.75(1200)\ + \ 300\ = \ 900\ + \ 300\ = \ 1200}\

So there is break-even point when firm produce 1200 units and sells them at Rs.1 each unit.

Graphical Presentation

Graphical Presentation

(vi) Solve \mathbf{(a)\ x\ -\ 2\lbrack 3}\mathbf{x\ -\ 2(x\ + \ 1)\rbrack\ + \ 5\ = \ 16\ \ \ (b)\ 4(3}\mathbf{x\ -\ 2)\ = \ 7(2\ -\ 5}\mathbf{x)\ -\ 5}\mathbf{x}\

\mathbf{(a)\ x\ -\ 2\lbrack 3}\mathbf{x\ -\ 2}\left( \mathbf{x\ + \ 1} \right)\mathbf{\rbrack\ + \ 5\ = \ 16}\

Solution:

\mathbf{x\ -\ 2\lbrack 3}\mathbf{x\ -\ 2}\mathbf{x - 2\rbrack + \ 5\ = \ 16}\

\mathbf{x\ -\ 2}\left\lbrack \mathbf{x - 2} \right\rbrack\mathbf{+ 5\ = \ 16}\

\mathbf{x\ -\ 2}\mathbf{x + 4 + 5\ = \ 16}\

\mathbf{- x + 9\ = \ 16}\

\mathbf{- x\ = \ 16 - 9}\

\mathbf{- x\ = \ - 7}\

\mathbf{x\ = \ 7}\

\mathbf{(b)\ 4(3}\mathbf{x\ -\ 2)\ = \ 7(2\ -\ 5}\mathbf{x)\ -\ 5}\mathbf{x}\

Solution:

\mathbf{4(3}\mathbf{x\ -\ 2)\ = \ 7(2\ -\ 5}\mathbf{x)\ -\ 5}\mathbf{x}\

\mathbf{12}\mathbf{x - 8 = 14 - 35}\mathbf{x - 5}\mathbf{x}\

\mathbf{12}\mathbf{x - 8 = 14 - 40}\mathbf{x}\

\mathbf{12}\mathbf{x + 40}\mathbf{x = 14 + 8}\

\mathbf{52}\mathbf{x = 22}\

\mathbf{x =}\frac{\mathbf{22}}{\mathbf{52}}\

\mathbf{x =}\frac{\mathbf{11}}{\mathbf{26}}\

(vii) Solve the following equation by using Quadratic formula:

\frac{\mathbf{y}^{\mathbf{2}}}{\mathbf{2}}\mathbf{- \ }\frac{\mathbf{y}}{\mathbf{6}}\mathbf{= \ }\frac{\mathbf{1}}{\mathbf{12}}\

Solution:

\frac{\mathbf{y}^{\mathbf{2}}}{\mathbf{2}}\mathbf{- \ }\frac{\mathbf{y}}{\mathbf{6}}\mathbf{= \ }\frac{\mathbf{1}}{\mathbf{12}}\

Multiply both sides by 12

\mathbf{12\ }\left\langle \frac{\mathbf{y}^{\mathbf{2}}}{\mathbf{2}} \right\rangle\mathbf{- \ 12}\left\langle \frac{\mathbf{y}}{\mathbf{6}} \right\rangle\mathbf{= \ 12}\left\langle \frac{\mathbf{1}}{\mathbf{12}} \right\rangle\

\mathbf{6}\mathbf{y²\ - \ 2}\mathbf{y\ = \ 1}\

\mathbf{6}\mathbf{y²\ - \ 2}\mathbf{y\ - \ 1 = \ 0}\

Apply quadratic formula

a= 6, b= -2, c = -1

\mathbf{x}\mathbf{=}\frac{\mathbf{-}\mathbf{b}\mathbf{\pm}\sqrt{\mathbf{b}^{\mathbf{2}}\mathbf{- 4}\mathbf{ac}}}{\mathbf{2}\mathbf{a}}\

\mathbf{x}\mathbf{=}\frac{\mathbf{2 \pm}\sqrt{\mathbf{- 2}^{\mathbf{2}}\mathbf{- 4}\left( \mathbf{6} \right)\mathbf{( - 1)}}}{\mathbf{2}\mathbf{(6)}}\

\mathbf{x}\mathbf{=}\frac{\mathbf{2 \pm 5.3}}{\mathbf{12}}\

\mathbf{x}\mathbf{=}\frac{\mathbf{2 + 5.3}}{\mathbf{12}} \textbf{=}\mathbf{x}\mathbf{=}\frac{\mathbf{7.3}}{\mathbf{12}} \textbf{=0.6084}

\mathbf{x}\mathbf{=}\frac{\mathbf{2 - 5.3}}{\mathbf{12}} \textbf{=}\mathbf{x}\mathbf{=}\frac{\mathbf{- 3.3}}{\mathbf{12}} \textbf{=}(\mathbf{- 0.275}\

So S.S {0.6084, -0.275}

(viii) Find inverse of the following matrix:

(a) \begin{bmatrix}\mathbf{4} & \mathbf{9} \\\mathbf{7} & \mathbf{6} \\\end{bmatrix}\

(b) \begin{bmatrix}\mathbf{1} & \mathbf{0} \\\mathbf{0} & \mathbf{1} \\\end{bmatrix}\

Solution

(a)

\mathbf{As\ we\ know\ that\ }\mathbf{A}^{\mathbf{- 1}}\mathbf{=}\frac{\mathbf{Adj\ A}}{\left| \mathbf{A} \right|}\

Where

\mathbf{Adj\ A =}\begin{bmatrix}\mathbf{6} & \mathbf{- 9} \\\mathbf{- 7} & \mathbf{4} \\\end{bmatrix}\ &

\left| \mathbf{A} \right|\mathbf{= 4\ x\ 6 - 9\ x\ 7 = 24 - 63 = - 39}\

\mathbf{A}^{\mathbf{- 1}}\mathbf{=}\frac{\mathbf{Adj\ A}}{\left| \mathbf{A} \right|}\mathbf{= \ }\mathbf{A}^{\mathbf{-1}}\mathbf{=}\frac{\begin{bmatrix}\mathbf{6} & \mathbf{- 9} \\\mathbf{- 7} & \mathbf{4} \\\end{bmatrix}\mathbf{\ }}{\mathbf{- 39}} \textbf{=}\mathbf{A}^{\mathbf{- 1}}\mathbf{=}\frac{\mathbf{1}}{\mathbf{- 39}}\mathbf{\ }\begin{bmatrix}\mathbf{6} & \mathbf{- 9} \\\mathbf{- 7} & \mathbf{4} \\\end{bmatrix}\

(b)

\mathbf{As\ we\ know\ that\ }\mathbf{A}^{\mathbf{- 1}}\mathbf{=}\frac{\mathbf{Adj\ A}}{\left| \mathbf{A} \right|}\textbf{Where} \mathbf{Adj\ A =}\begin{bmatrix}\mathbf{1} & \mathbf{- 0} \\\mathbf{- 0} & \mathbf{1} \\\end{bmatrix} \textbf{\&}\left| \mathbf{A} \right|\mathbf{= 1\ x\ 1 - 0 = 1}\

\mathbf{A}^{\mathbf{- 1}}\mathbf{=}\frac{\mathbf{Adj\ A}}{\left| \mathbf{A} \right|}\mathbf{= \ }\mathbf{A}^{\mathbf{-1}}\mathbf{=}\frac{\begin{bmatrix}\mathbf{1} & \mathbf{- 0} \\\mathbf{- 0} & \mathbf{1} \\\end{bmatrix}\mathbf{\ }}{\mathbf{1}}) \textbf{=}\mathbf{A}^{\mathbf{- 1}}\mathbf{=}\frac{\mathbf{1}}{\mathbf{1}}\mathbf{\ }\begin{bmatrix}\mathbf{1} & \mathbf{- 0} \\\mathbf{- 0} & \mathbf{1} \\\end{bmatrix}\

(ix) Find the determinant of the following matrix & explain whether it is a singular or non singular matrix.

\begin{bmatrix}\mathbf{4} & \mathbf{- 3} \\\mathbf{- 4} & \mathbf{2} \\\end{bmatrix}\

Solution

\left| \mathbf{A} \right|\mathbf{= 4\ x\ 2 -}\left( \mathbf{- 3} \right)\mathbf{\ ( - 4) = 8 - 12 = - 4}\

\left| \mathbf{A} \right|\mathbf{\neq 0\ so\ it\ is\ non\ singular\ matrix}\

(x) Solve the following equation by Crammers law.

2x – 6y = – 12

3x – 2y = -4

Solution:

\begin{bmatrix}\mathbf{2} & \mathbf{- 6} \\\mathbf{3} & \mathbf{- 2} \\\end{bmatrix}\ \begin{bmatrix}\mathbf{x} \\\mathbf{y} \\\end{bmatrix} \textbf{=} \begin{bmatrix}\mathbf{- 12} \\\mathbf{- 4} \\\end{bmatrix}\

As we know that:

\mathbf{x =}\frac{\left| \mathbf{Ax} \right|}{\left| \mathbf{A} \right|}\textbf{\&}\mathbf{y =}\frac{\left| \mathbf{Ay} \right|}{\left| \mathbf{A} \right|}\textbf{where A =}\begin{bmatrix}\mathbf{2} & \mathbf{- 6} \\\mathbf{3} & \mathbf{- 2} \\\end{bmatrix}\textbf{,} \mathbf{Ax =}\begin{bmatrix}\mathbf{- 12} & \mathbf{- 6} \\\mathbf{- 4} & \mathbf{- 2} \\\end{bmatrix} \textbf{\&} \mathbf{Ay =}\begin{bmatrix}\mathbf{2} & \mathbf{- 12} \\\mathbf{3} & \mathbf{- 4} \\\end{bmatrix}\

\left| \mathbf{A} \right|\mathbf{= 2\ }\left( \mathbf{- 2} \right)\mathbf{-}\left( \mathbf{- 6} \right)\mathbf{3 = - 4 + 18 = 14\ }\

\left| \mathbf{Ax} \right|\mathbf{= - 12\ }\left( \mathbf{- 2} \right)\mathbf{-}\left( \mathbf{- 6} \right)\mathbf{( - 4) = 24 + 24 = 48\ }\

\left| \mathbf{Ay} \right|\mathbf{= 2\ }\left( \mathbf{- 4} \right)\mathbf{-}\left( \mathbf{- 12} \right)\mathbf{3 = - 8 + 36 = 28\ }\

\mathbf{x =}\frac{\left| \mathbf{Ax} \right|}{\left| \mathbf{A} \right|}\mathbf{= \ }\frac{\mathbf{48}}{\mathbf{14}}\mathbf{= 3.429}\

\mathbf{y =}\frac{\left| \mathbf{Ay} \right|}{\left| \mathbf{A} \right|}\mathbf{= \ }\frac{\mathbf{28}}{\mathbf{14}}\mathbf{= 2}\

 (xi) Simplify the following: \textbf{{(11101111)2 -- (10001)2} -- {(1111000)2 -- (1000)2}}

Binary Solution

\textbf{Answer is (1101110)2}

Extensive Questions

Section C

Attempt any two questions. All questions carry equal marks (2 x 8) = 16

Q.3 a. If the price of 50 ready-made shirts is Rs. 3652/- then what is the price of 85 such shirts?

b. If ratio of cars and trucks is 7:2 and there are 26 trucks, how many cars are there?

Solution

(a)

\mathbf{Price\ of\ 50\ ready - made\ shirts\ = \ 3652}\

\mathbf{Price\ of\ one\ shirt\ =}\frac{\mathbf{3652}}{\mathbf{50}}\mathbf{\ = \ 73.04}\

\mathbf{Price\ of\ 85\ shirts\ = \ 85\ \times \ 73.04\ = \ 6208.4}\

(b) 7:2::x:26

\mathbf{7 \times 26\ = \ 2}\mathbf{x\ or\ 2}\mathbf{x\ = \ 182\ }\

\mathbf{X\ =}\frac{\mathbf{182}}{\mathbf{2}}\

X = 91 so there are 91 cars

Q.4 a. Find the value of motor car costing Rs. 250,000/- at the end of 7 years. If depreciation at the rate of 7 ½ % is written off on the value at the commencement of each year.

b. Convert into decimal (i) (1001)2   (ii) (111011)2

Solution

  • Cost C = 250,000, n = 7, i= 7 ½ % = 0.075

There are two formulas to find value of the asset after n years

  • Depreciated value of the asset after n years = C – nD

Where C = cost, n =number of year passed, D = Depreciation amount

  • Depreciated value of the asset after n years = \mathbf{C(1\ -\ r)}^{\mathbf{n}}\

Where C = cost, r = rate of depreciation, n= Number of years passed

According to available data we will use 2nd formula here:

Depreciated value of the asset after n years = \mathbf{C(1\ -\ r)}^{\mathbf{n}}\

Depreciated value of the asset after n years = \mathbf{250,000(1\ -\ 0.075)}^{\mathbf{7}}\

Depreciated value of the asset after n years = \mathbf{250,000(0.5794)}\

Depreciated value of the asset after n years = \mathbf{144850}\

(b) (i) Binary number given is (1001)₂

Solution:

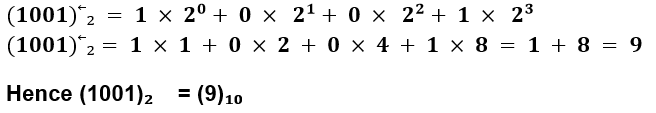
(ii) Binary number given is (111011)₂

Solution:

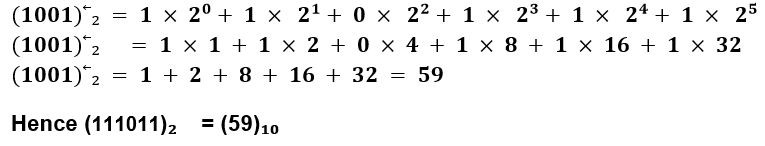
Q.5 a. What is the interest on Rs. 1880.90 for one year @ 5 ½ %?

b. Find the compound interest of principal amount Rs. 50,000/- at the rate of 5% for 3 ¾ years.

Solution (a)

\mathbf{P\ = \ 1880.90,\ N\ = \ 1,\ I = \ 5\ ½\ \%\ = \ 5.5\%\ = \ }\frac{\mathbf{5.5}}{\mathbf{100}}\mathbf{\ = \ 0.055,\ S.I\ = \ ?}\

\mathbf{S.I\ = \ PIN}\

\mathbf{S.I\ = \ 1880.90\ \times \ 1\ \times \ 0.055}\

\mathbf{S.I\ = \ 103.4495\ }\

Solution (b)

\mathbf{P\ = \ 50,000,\ n\ = \ 3\ ¾\ quarter\ = \ }\left( \mathbf{3\ \times \ 4} \right)\mathbf{+ \ 3\ = \ 15,\ I = \ 5\ \%\ =}\frac{\mathbf{5}}{\mathbf{4}}\mathbf{\ = 1.25\ =}\frac{\mathbf{\ 1.25}}{\mathbf{100}}\mathbf{\ = \ 0.0125,\ C.I\ = ?}\

\mathbf{C.I\ = \ P(1 + i)}^{\mathbf{n}}\mathbf{- \ p}\

\mathbf{C.I = \ 50,000(1.2048) - \ 50,000}\

\mathbf{C.I = \ 60240 - \ 50,000}\

\mathbf{C.I = \ 10240}\

You may also interested in the following:

Business Mathematics

Business Statistics Solved Paper FBISE 2012 ICOM II, MCQS, Short Questions, Extensive Questions

Business Statistics Solved Paper FBISE 2013 ICOM II, MCQS, Short Questions, Extensive Questions

Business Statistics Solved Paper FBISE 2015 ICOM II, MCQS, Short Questions, Extensive Questions

Business Statistics Solved Paper FBISE 2016 ICOM II, MCQS, Short Questions, Extensive Questions

Business Statistics Solved Paper FBISE 2016 2nd Annual ICOM II, MCQS, Short Questions, Extensive Questions

Business Statistics Solved Paper FBISE 2017 ICOM II, MCQS, Short Questions, Extensive Questions

Business Statistics Solved Paper FBISE 2017 2nd Annual ICOM II, MCQS, Short Questions, Extensive Questions

Business Statistics Solved Paper FBISE 2018 ICOM II, MCQS, Short Questions, Extensive Questions

Consignment Account, Consignor or principal, Consignee or agent, Complete Analysis with Journal Entries, Theoretical Aspect, MCQ’s and Practical Examples

Depreciation, Reasons of Depreciation, Methods of Depreciation, Straight Line/ Original Cost/Fixed Instalment Method, Diminishing/Declining/Reducing Balance Method.

Introduction to Statistics Basic Important Concepts

Measures of Central Tendency, Arithmetic Mean, Median, Mode, Harmonic, Geometric Mean

Related Posts

Leave a Comment

Your email address will not be published. Required fields are marked *