In this post, we are going to discuss correlation coefficient, types, properties, importance and important formulas for Correlation Coefficient and also cover correlation coefficient with theoretical perspective.
Table of Contents
Correlation Coefficient
The correlation coefficient is a statistical measure that calculates or quantifies the relationship or strength and direction of the linear relationship between two variables. In other words, it indicates how closely the values of two variables move together. Correlation Coefficient always denoted by the symbol “r” and it’s answer ranges between -1 and 1. It’s answer has five possibilities:
Types of Correlation
1. Perfectly Positive
1: Perfectly Positive: A correlation coefficient of +1 indicates a perfect positive linear relationship which means as one variable increases, the other variable also increases proportionally or vice versa.

2. Positive
2: Positive: A correlation coefficient ranges between 0 and +1 indicates a positive relationship which means as one variable increases, the other also increases but not proportionally or vice versa.

3. Perfectly Negative
3: Perfectly Negative: A correlation coefficient of -1 indicates a perfect negative linear relationship which means as one variable increases, the other variable decreases proportionally or vice versa.

4. Negative
4: Negative: A correlation coefficient ranges between 0 and -1 indicates a negative relationship which means as one variable increases, the other decreases but not proportionally or vice versa.

5. Zero
5: Zero: A correlation coefficient close to 0 or exactly 0 indicates a weak or no linear relationship between the variables.
Properties of the Correlation Coefficient
1. The correlation coefficient does not change the measurement scale. That is, if the height is expressed in meters or feet, the correlation coefficient does not change.
2. The sign of the correlation coefficient is the same as the covariance.
3. The linear correlation coefficient is a real number between −1 and 1. −1 ≤ r ≤ 1
4. The Correlation Coefficient -1 means a strong perfectly negative relation.
5. The Correlation Coefficient +1 means a perfectly positive relation.
6. The Correlation Coefficient 0<r<1 means a positive relation.
7. The Correlation Coefficient -1<r<0 means a negative relation.
8. The Correlation Coefficient 0 means no relation.
9. The Correlation Coefficient is symmetric, which means the Correlation between X and Y equals to Correlation Coefficient between Y and X.
10. Non-linearity property of the correlation coefficient is that it tells best about linear relations. In non-linear relations, it is inaccurate in prediction.
11. Causation property of the Correlation Coefficient is that it only quantifies the relationships, it does not tell the cause of the relationship.
12. It is geometric mean of two regression coefficients
![]()
Importance
Correlation coefficient is widely used in data analysis, research, business predictions such as investments and many other fields you name it. One important reality must be considered that it does not mean that one variable cause changes to other variable, there may be other hidden factors or variables responsible for it so we can say that it does not imply causation.
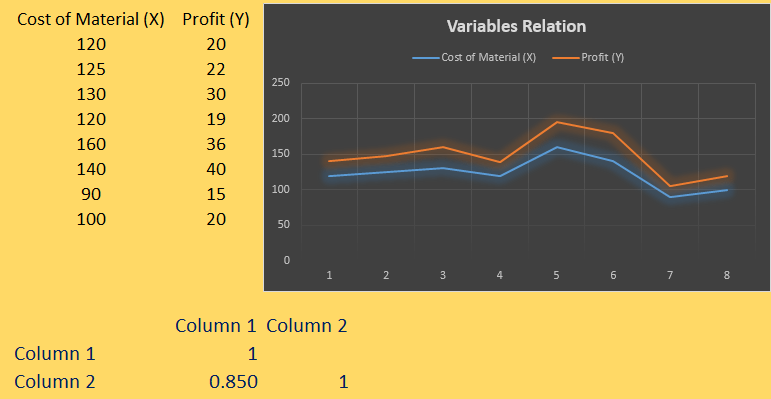
Important Formulas for Correlation Coefficient
Formula 1
![]()
![]()
![]()
![]()
![]()
Formula 2
![]()
Formula 3
![Rendered by QuickLaTeX.com \[ r_{xy} = \frac{\sum XY - \frac{(\sum X)(\sum Y)}{n}}{\sqrt{\left\lbrack \sum X^{2} - \frac{(\sum X)^{2}}{n} \right\rbrack\left\lbrack \sum Y^{2} - \frac{(\sum Y)^{2}}{n} \right\rbrack}} \]](https://bcfeducation.com/wp-content/ql-cache/quicklatex.com-55bfbd80c03283ec4e2e9c4a84eac04f_l3.png)
Formula 4
![]()
Formula 5
![Rendered by QuickLaTeX.com \[ r_{xy} = \frac{\sum XY - n\overline{X}\overline{Y}}{\sqrt{\left( \sum X^{2} - {n\left( \overline{X} \right)}^{2} \right)\left( \sum Y^{2} - {n\left( \overline{Y} \right)}^{2} \right)}} \]](https://bcfeducation.com/wp-content/ql-cache/quicklatex.com-65109bf64c39dc1ad287bf4b3361daf7_l3.png)
Formula 6
![]()
![]()
![]()
Their Formulas are Given Below:
![]()
Formula 7
![]()
![Rendered by QuickLaTeX.com \[ \frac{\sum D_{x}D_{y} - \frac{(\sum D_{x})(\sum D_{y})}{n}}{\sqrt{\left\lbrack \sum{D_{x}}^{2} - \frac{\left( \sum D_{x} \right)^{2}}{n} \right\rbrack\left\lbrack \sum{D_{y}}^{2} - \frac{\left( \sum D_{y} \right)^{2}}{n} \right\rbrack}}\ \]](https://bcfeducation.com/wp-content/ql-cache/quicklatex.com-a4bcff1565e83f54a656319b458482b0_l3.png)
Formula 8
![Rendered by QuickLaTeX.com \[ r_{xy} = \frac{n\sum D_{x}D_{y} - (\sum D_{x})(\sum D_{y})}{\sqrt{\left( n\sum{D_{x}}^{2} - \left( \sum D_{x} \right)^{2} \right)\left( n\sum{D_{y}}^{2} - \left( \sum D_{y} \right)^{2} \right)}}\ \]](https://bcfeducation.com/wp-content/ql-cache/quicklatex.com-a9442e33e8d6fcced05427da49608b25_l3.png)
![]()
Formula 9
![Rendered by QuickLaTeX.com \[ {r_{xy} = r}_{uv} = \frac{\sum UV - \frac{(\sum U)(\sum V)}{n}}{\sqrt{\left\lbrack \sum U^{2} - \frac{(\sum U)^{2}}{n} \right\rbrack\left\lbrack \sum V^{2} - \frac{(\sum V)^{2}}{n} \right\rbrack}}\]](https://bcfeducation.com/wp-content/ql-cache/quicklatex.com-14b776bad4f5bbbf1d2c6b97959a2857_l3.png)
Formula 10
![]()
Formula 11
![]()
![]()
![]()
You may also interested in the following:
Introduction to Statistics Basic Important Concepts
Measures of Central Tendency, Arithmetic Mean, Median, Mode, Harmonic, Geometric Mean
Business Mathematics and Statistics, Solved Paper 2007, Punjab University, BCOM,ADCI
Business Mathematics and Statistics, Solved Paper 2008, Punjab University, BCOM,ADCI
Business Statistics and Mathematics, Solved Paper 2009, Punjab University, BCOM,ADCI
Business Statistics and Mathematics, Solved Paper 2010, Punjab University, BCOM,ADCI
Business Statistics and Mathematics Solved Paper 2011, Punjab University, BCOM, ADC I







Thank You Sir