Chapter 8: How to calculate Net Present Value and Other Investment Criteria/Capital Budgeting Techniques

In this post, I am going to teach you that what are capital budgeting techniques, how net present value, profitability index, payback period, internal rate of return can be calculated & how all these put impact on investment criteria.

Introduction to Capital Budgeting Techniques

Net Present Value and other Investment Criteria such as Internal Rate of Return, Payback Period, and Profitability index are different concepts of Capital Budgeting Techniques. These all deal with future investment proposals. With the help of all the above techniques, we decide either to choose the project or leave to invest in the project.

Among all four above, Net Present Value and Internal Rate of Return are the two most common primary ways to estimate future profitability and these both have very important relations with each other which will be discussed later in this topic whereas profitability index and payback period are both secondary ways to assess the profitability.

Net Present Value NPV

Net present value is simply the net sum of present values of cash outflow or initial investment and future cash inflows. Cash outflow is our investment which we plan to invest in a certain investment proposal and cash inflows are those inflows that we expect to earn in the future for a certain time period.

For the calculation of net present value, we have to understand present value calculation by using present value tables or manual calculation. One thing you should remember is that if future cash inflows are same, then you can use the Present Value of Interest Factor of Annuity (PVIFA) otherwise Present Value Interest Factor PVIF.

Present value has vital importance in the concept of the time value of money which tells us that how much value is today for future cash flow because there are various factors those minimizes the value of money as time passes.

Acceptance Criteria of Investment under Net Present Value

If NPV = 0 means no profitability no loss

If NPV > 1 means profitability

If NPV < 1 means loss

Net Present Value Formula for Similar Cash Inflows:

$\mathbf{NPV = - Cash\ outflow + Cash\ Inflow(}\mathbf{PVIFA}_{\mathbf{i,n}}\mathbf{)}\$

Net Present Value Formula for No similar Cash Inflows

$\mathbf{NPV = - Cash\ outflow +}\frac{\mathbf{Cash\ Flow\ 1}}{\left( \mathbf{1 + i} \right)^{\mathbf{1}}}\mathbf{+}\frac{\mathbf{Cash\ Flow\ 2}}{\left( \mathbf{1 + i} \right)^{\mathbf{2}}}\mathbf{+}\frac{\mathbf{Cash\ Flow\ n}}{\mathbf{(1 + i)}^{\mathbf{n}}}\$

The formula for PVIFA Present Value of Interest Factor of Annuity

$\mathbf{PVIFA =}\left\lbrack \frac{\mathbf{1 -}\mathbf{(1 + i)}^{\mathbf{- n}}}{\mathbf{i}} \right\rbrack\$

Formula for PVIF Present Value of Interest Factor

$\mathbf{PVIF =}\left( \mathbf{1 + i} \right)^{\mathbf{- n}}\mathbf{\ or\ }\frac{\mathbf{1}}{\left( \mathbf{1 + i} \right)^{\mathbf{n}}}\$

Capital Budgeting Techniques Net Present Value

Calculation of NPV with Similar Cash Flows

Practical Questions for Understanding

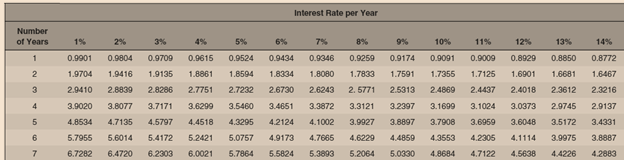
Question 1: If opportunity cost of capital is 10%, Calculate NPV of both projects, In case of mutually exclusive projects, which project is better to invest?

Year	Project A	Project B
0	-500	-500
1	400	450
2	400	450
3	400	450
4	400	450
5	400	450

Solution:

$\mathbf{NPV\ Project\ A = CashoutflowProject\ A + Cash\ Inflow\ Project\ A(}\mathbf{PVIFA}_{\mathbf{i,n}}\mathbf{)}\$

$\mathbf{NPV\ Project\ A = - 500 + 400\ (}\mathbf{PVIFA}_{\mathbf{0.10,5}}\mathbf{)}\$

$\mathbf{NPV\ Project\ A = - 500 + 400(3.790)}\$

$\mathbf{NPV\ Project\ A = - 500 + 1516 = 1016}\$

$\mathbf{NPV\ Project\ B = CashoutflowProject\ B + Cash\ InflowProject\ B(}\mathbf{PVIFA}_{\mathbf{i,n}}\mathbf{)}\$

$\mathbf{NPV\ Project\ B = - 500 + 450\ (}\mathbf{PVIFA}_{\mathbf{0.10,5}}\mathbf{)}\$

$\mathbf{NPV\ Project\ B = - 500 + 450(3.790)}\$

$\mathbf{NPV\ Project\ B = - 500 + 1705.5 = 1205.5}\$

$\mathbf{PVIFA\ at\ n = 5,\ i = 0.10}\$

$\mathbf{PVIFA =}\left\lbrack \frac{\mathbf{1 -}\mathbf{(1 + i)}^{\mathbf{- n}}}{\mathbf{i}} \right\rbrack\$

$\mathbf{PVIFA =}\left\lbrack \frac{\mathbf{1 -}\mathbf{(1 + 0.10)}^{\mathbf{- 5}}}{\mathbf{0.10}} \right\rbrack\mathbf{= 3.790}\$

Project B is worth more because NPV of Project B is greater than the NPV of Project A

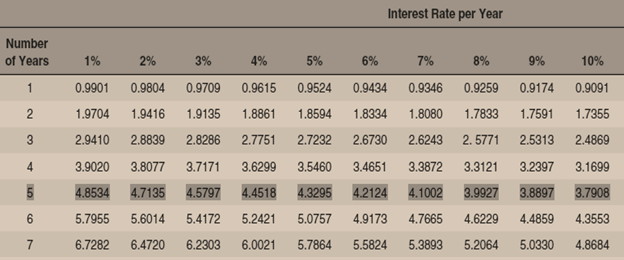
Calculation of NPV with Non Similar Cash Flows

Practical Questions for Understanding

Question 2: Calculate Net Present Value for the following cash flows if opportunity cost is 15%.

Year	1	2	3	4
Cash Flows	2500	1500	2700	3000

Solution:

$\mathbf{NPV = Cash\ outflow +}\frac{\mathbf{Cash\ Flow\ 1}}{\left( \mathbf{1 + i} \right)^{\mathbf{1}}}\mathbf{+}\frac{\mathbf{Cash\ Flow\ 2}}{\left( \mathbf{1 + i} \right)^{\mathbf{2}}}\mathbf{+}\frac{\mathbf{Cash\ Flow\ 3}}{\mathbf{(1 + i)}^{\mathbf{3}}}\mathbf{+}\frac{\mathbf{Cash\ Flow\ 4}}{\mathbf{(1 + i)}^{\mathbf{4}}}\$

$\mathbf{NPV = - 5000 +}\frac{\mathbf{2500}}{\left( \mathbf{1 + 0.15} \right)^{\mathbf{1}}}\mathbf{+}\frac{\mathbf{1500}}{\left( \mathbf{1 + 0.15} \right)^{\mathbf{2}}}\mathbf{+}\frac{\mathbf{2700}}{\mathbf{(1 + 0.15)}^{\mathbf{3}}}\mathbf{+}\frac{\mathbf{3000}}{\mathbf{(1 + 0.15)}^{\mathbf{4}}}\$

$\mathbf{NPV = - 5000 + 2173.91 + 1134.21 + 1175.29 + 1715.25}\$

$\mathbf{NPV = 1198.66}\$

NPV Net Present Value (Decommission Case)

Practical Questions for Understanding

Question 3: A cement plant will cost to you $3.4 billion to build and then will produce cash flows of $350 million a year for 16 years. After that period, it must be decommissioned at a cost of $800 million. What is project NPV if the discount rate is 8%?

Solution:

$\mathbf{NPV = Cash\ outflow + Cash\ Inflow}\left( \mathbf{PVIFA}_{\mathbf{i,n}} \right)\mathbf{-}\frac{\mathbf{Decommissioned\ Value}}{\left( \mathbf{1 + i} \right)^{\mathbf{n}}}\$

$\mathbf{NPV = Cash\ outflow + Cash\ Inflow}\left( \mathbf{PVIFA}_{\mathbf{0.08,16}} \right)\mathbf{-}\frac{\mathbf{Decommissioned\ Value}}{\left( \mathbf{1 + i} \right)^{\mathbf{n}}}\$

$\mathbf{NPV = - 3.4 + 0.350}\left( \mathbf{8.851} \right)\mathbf{-}\frac{\mathbf{0.8}}{\left( \mathbf{1 + 0.08} \right)^{\mathbf{16}}}\$

$\mathbf{NPV = - 3.4 + 3.09785 - 0.23351}\$

$\mathbf{NPV = - 0.53566\ billion}\$

$\mathbf{PVIFA\ at\ n = 16,\ i = 0.08}\$

$\mathbf{PVIFA =}\left\lbrack \frac{\mathbf{1 -}\mathbf{(1 + i)}^{\mathbf{- n}}}{\mathbf{i}} \right\rbrack\$

$\mathbf{PVIFA =}\left\lbrack \frac{\mathbf{1 -}\mathbf{(1 + 0.08)}^{\mathbf{- 16}}}{\mathbf{0.08}} \right\rbrack\mathbf{= 8.851}\$

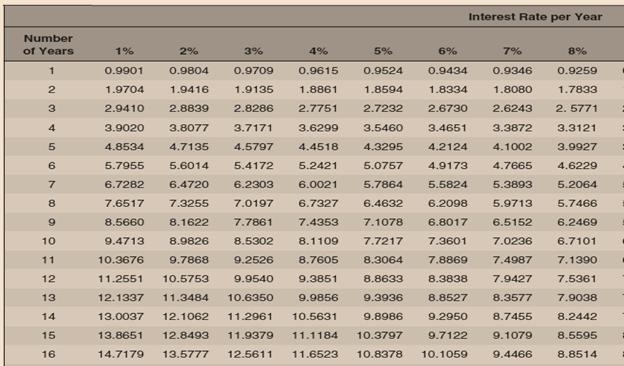
Internal Rate of Return

Practical Questions for Understanding

Question 4: Calculate Internal Rate of Return for the following two projects & also calculate their respective NPV’s if opportunity cost is 12%.

Year	Cash Flows Project A	Cash Flows Project B
0	-24000	-20000
1	8000	0
2	8000	4500
3	8000	5000
4	8000	0
5	8000	8000
6	8000	12000

Solution:

There is no such formula to calculate internal rate of return manually. We can use financial calculator, MS Excel or we can calculate it through trial and error method. Here we will use MS Excel to calculate it.

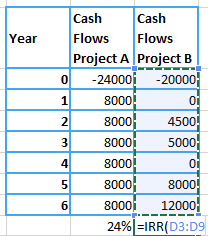
Internal Rate of Return for Project A = 24%

Internal Rate of Return for Project B = 9%

$\mathbf{NPVProject\ A = Cash\ outflow + Cash\ Inflow(}\mathbf{PVIFA}_{\mathbf{12\%,6}}\mathbf{)}\text{~}\$

$\mathbf{NPVProject\ A = - 24000 + 8000(}\mathbf{PVIFA}_{\mathbf{12\%,6}}\mathbf{)}\text{~}\$

$\mathbf{NPVProject\ A = - 24000 + 8000(4.111)}\$

$\mathbf{NPVProject\ A = - 24000 + 32888}\$

$\mathbf{NPVProject\ A = 8888}\$

$\mathbf{PVIFA\ at\ n = 6,\ i = 0.12}\$

$\mathbf{PVIFA =}\left\lbrack \frac{\mathbf{1 -}\mathbf{(1 + i)}^{\mathbf{- n}}}{\mathbf{i}} \right\rbrack\$

$\mathbf{PVIFA =}\left\lbrack \frac{\mathbf{1 -}\mathbf{(1 + 0.12)}^{\mathbf{- 6}}}{\mathbf{0.12}} \right\rbrack\mathbf{= 4.111}\$

$\mathbf{NPVProject\ B = Cash\ outflow +}\frac{\mathbf{Cash\ Flow\ 1}}{\left( \mathbf{1 + i} \right)^{\mathbf{1}}}\mathbf{+}\frac{\mathbf{Cash\ Flow\ 2}}{\left( \mathbf{1 + i} \right)^{\mathbf{2}}}\mathbf{+}\frac{\mathbf{Cash\ Flow\ 3}}{\mathbf{(1 + i)}^{\mathbf{3}}}\mathbf{+}\frac{\mathbf{Cash\ Flow\ 4}}{\mathbf{(1 + i)}^{\mathbf{4}}}\mathbf{+}\frac{\mathbf{Cash\ Flow\ 5}}{\mathbf{(1 + i)}^{\mathbf{5}}}\mathbf{+}\frac{\mathbf{Cash\ Flow\ 6}}{\mathbf{(1 + i)}^{\mathbf{6}}}\$

$\mathbf{NPVProject\ B = - 20000 +}\frac{\mathbf{0}}{\left( \mathbf{1 + 0.12} \right)^{\mathbf{1}}}\mathbf{+}\frac{\mathbf{4500}}{\left( \mathbf{1 + 0.12} \right)^{\mathbf{2}}}\mathbf{+}\frac{\mathbf{5000}}{\mathbf{(1 + 0.12)}^{\mathbf{3}}}\mathbf{+}\frac{\mathbf{0}}{\mathbf{(1 + 0.12)}^{\mathbf{4}}}\mathbf{+}\frac{\mathbf{8000}}{\mathbf{(1 + 0.12)}^{\mathbf{5}}}\mathbf{+}\frac{\mathbf{12000}}{\mathbf{(1 + 0.12)}^{\mathbf{6}}}\$

$\mathbf{NPVProject\ B = - 20000 + 0 + 3587.37 + 3558.90 + 0 + 4539.41 + 6079.57}\$

NPV Project B = – 2234.75

Payback Period

Practical Questions for Understanding

Question 5: Calculate payback period in both cases of investment. Firm will accept the project A if its payback period is less than 4 years & will accept the project B if its payback period is less than 4 years. Evaluate the results.

Solution:

Payback Period for Project A which has similar cash inflows:

$\mathbf{Payback\ period\ for\ Project\ A =}\frac{\mathbf{Initial\ Cash\ Outflow}}{\mathbf{Cash\ Inflow}}$

$\mathbf{Payback\ period\ for\ Project\ A =}\frac{\mathbf{24000}}{\mathbf{8000}}\mathbf{= 3\ years}\$

Firm will accept the project because payback period is less than 4 years.

Payback Period for Project B which has non-similar cash inflows:

Formula

$\mathbf{Payback\ Period = a + \ }\frac{\mathbf{(b - c)}}{\mathbf{d}}\$

$\mathbf{Payback\ Period = 5 + \ }\frac{\mathbf{(20000 - 17500)}}{\mathbf{12000}}\$

$\mathbf{Payback\ Period = 5 + 0.2084}\$

$\mathbf{Payback\ Period = 5.2084}\$

Project is not acceptable for the firm because actual payback period is greater than 4 years.

Profitability Index

Practical Questions for Understanding

Question 6: Calculate profitability index in both cases of investment.

Solution:

Profitability Index for Project A & B:

$\mathbf{Profitability\ Index\ for\ Project\ A =}\frac{\mathbf{NPV\ of\ Project\ A}}{\mathbf{Initial\ Investment\ of\ Project\ A}}\$

$\mathbf{Profitability\ Index\ for\ Project\ A =}\frac{\mathbf{8888}}{\mathbf{24000}}\mathbf{= 0.370}\$

$\mathbf{Profitability\ Index\ for\ Project\ B =}\frac{\mathbf{NPV\ of\ Project\ B}}{\mathbf{Initial\ Investment\ of\ Project\ B}}\$

$\mathbf{Profitability\ Index\ for\ Project\ B =}\frac{\mathbf{- 2234.75}}{\mathbf{20000}}\mathbf{= - 0.1117375}\$

Note: NPV of Project A = 8888 & NPV of Project B = -2234.75 calculated above

Equivalent Annual Annuity

Practical Questions for Understanding

Present Value of Cost in Case of Buying

Question 7: A firm can lease a machine for 5 years at a cost of $40,000 annually. It can instead buy a machine at a cost of $90,000, with annual maintenance expenses of $11,000. The machine will be sold at the end of 5 years for $22,000. Which is the better option if the discount rate is 12%?

Solution:

$\mathbf{Present\ Values\ of\ Costs = Initial\ Cost + Expenses}\left( \mathbf{PVIFA}_{\mathbf{i,n}} \right)\mathbf{-}\frac{\mathbf{Scrap\ Value}}{\left( \mathbf{1 + i} \right)^{\mathbf{n}}}\text{~}\$

$\mathbf{Present\ Values\ of\ Costs = 90000 + 11000}\left( \mathbf{PVIFA}_{\mathbf{12\%,5}} \right)\mathbf{-}\frac{\mathbf{22000}}{\left( \mathbf{1 + 0.12} \right)^{\mathbf{5}}}\text{~}\$

$\mathbf{Present\ Values\ of\ Costs = 90000 + 11000}\left( \mathbf{3.604} \right)\mathbf{- 12483.390}\text{~}\$

$\mathbf{Present\ Values\ of\ Costs = 90000 + 39644 - 12483.390 = 1,17,160.61}\text{~~}\$

Present Value of Cost in Case of Lease

$\mathbf{Present\ Values\ of\ Costs = Lease\ Expenses}\left( \mathbf{PVIFA}_{\mathbf{12\%,5}} \right)\$

$\mathbf{Present\ Values\ of\ Costs = 40000}\left( \mathbf{3.604} \right)\mathbf{= 1,44,160}\$

Option for buying a machine is better than to get on lease because present values of buying is less than present value of lease.

Calculation of PVIFA

$\mathbf{PVIFA\ at\ n = 5,\ i = 0.12}\$

$\mathbf{PVIFA =}\left\lbrack \frac{\mathbf{1 -}\mathbf{(1 + i)}^{\mathbf{- n}}}{\mathbf{i}} \right\rbrack\$

$\mathbf{PVIFA =}\left\lbrack \frac{\mathbf{1 -}\mathbf{(1 + 0.12)}^{\mathbf{- 5}}}{\mathbf{0.12}} \right\rbrack\mathbf{= 3.604}\$

Important Questions of Previous Papers for Practice

Question 1: A forklift will last for only 2 more years. It costs $5,000 a year to maintain. For $20,000 you can buy a new lift that can last for 10 years and should require maintenance costs of only $2,000 a year.

a. If the discount rate is 4% per year, should you replace the forklift?

b. What if the discount rate is 12% per year? Why does your answer change?

Questions 2: Here are the cash flows for two mutually exclusive projects:

Which project would you choose if the opportunity cost of capital is 2%?
Which would you choose if the opportunity cost of capital is 12%?
Why does your answer change?

Follow Book Corporate Finance BREALEY MYERS MARCUS

Question 3: Consider projects A and B:

Calculate IRRs for A and B. Which project does the IRR rule suggest is best? Which project is really best?

Question 4: A new computer system will require an initial outlay of $20,000, but it will increase the firm’s cash flows by $4,000 a year for each of the next 8 years. Is the system worth installing if the required rate of return is 9%? What if it is 14%? How high can the discount rate be before you would reject the project?

Question 5: Consider this project with an internal rate of return of 13.1%. Should you accept Project the project if the discount rate is 12%?

Year	Cash Flows
0	+$100
1	-60
2	-60

Follow Book Corporate Finance BREALEY MYERS MARCUS

Question 6: a. What is the payback period on each of the following projects?

		Cash Flows
Project	Year	0	1	2	3	4
A		-5000	+1000	+1000	+3000	0
B		-1000	0	+1000	+2000	+3000
C		-5000	+1000	+1000	+3000	+5000

b. Given that you wish to use the payback rule with a cutoff period of 2 years, which projects would you accept?

c. If you use a cutoff period of 3 years, which projects would you accept?

d. If the opportunity cost of capital is 10%, which projects have positive NPVs?

e. “Payback gives too much weight to cash flows that occur after the cutoff date.” True or false?

Question 7: Consider the following projects:

Project	C0	C1	C2
A	-$2100	+$2000	+$1200
B	-2100	+1440	+1728

a. Calculate the profitability index for A and B assuming a 22% opportunity cost of capital.

b. Use the profitability index rule to determine which project(s) you should accept

To Follow the video lecture about Capital Budgeting Techniques click the link below:

To follow Statistics Blog Posts Click the link : https://bcfeducation.com/category/statistics/

To follow IGCSE/O Level Business Blog Posts Click the link : https://bcfeducation.com/category/business/

To follow Financial Management Blog Posts Click the link : https://bcfeducation.com/category/financial-management/

To follow IGCSE/O Level Accounting Blog Posts Click the link : https://bcfeducation.com/category/olevel-accounting/

Introduction to Capital Budgeting Techniques

Net Present Value NPV

Net Present Value Formula for Similar Cash Inflows:

Net Present Value Formula for No similar Cash Inflows

The formula for PVIFA Present Value of Interest Factor of Annuity

Formula for PVIF Present Value of Interest Factor

Calculation of NPV with Similar Cash Flows

Practical Questions for Understanding

Calculation of NPV with Non Similar Cash Flows

Practical Questions for Understanding

NPV Net Present Value (Decommission Case)

Practical Questions for Understanding

Internal Rate of Return

Practical Questions for Understanding

Payback Period

Practical Questions for Understanding

Payback Period for Project A which has similar cash inflows:

Payback Period for Project B which has non-similar cash inflows:

Profitability Index

Practical Questions for Understanding

Equivalent Annual Annuity

Present Value of Cost in Case of Buying

Present Value of Cost in Case of Lease

Important Questions of Previous Papers for Practice

Leave a Comment Cancel Reply